ホーム
高校数学
数学III・C

数学III・C

  1. 数学III
    1. 関数
      1. 分数関数・無理関数
        1. 分数関数 \(\displaystyle \quad y = \dfrac{ax + b}{cx + d} \)
      2. 無理関数 \( \quad y = \sqrt{ax + b} \)
      3. 逆関数・合成関数
        1. 逆関数
        2. 合成関数
    2. 極限
      1. 数列の極限
        1. 数列の極限
        2. 無限等比数列の極限
      2. 無限級数
        1. 無限級数の収束・発散
        2. 無限等比級数 \(\displaystyle \quad \sum_{n = 1}^\infty ar^{n – 1},\ a \neq 0 \)
      3. 関数の極限
        1. 関数の極限
        2. 極限に関する性質
        3. 三角関数の極限
        4. 関数の連続・不連続
        5. 中間値の定理
    3. 微分法
      1. 微分法の基本
        1. 微分係数
        2. 微分可能と連続、導関数の公式
      2. 三角、指数、対数関数の導関数
        1. 三角関数の導関数
        2. 指数・対数関数の導関数
        3. 対数微分法
    4. 微分法の応用
    5. 積分法
    6. 積分法の応用
  2. 数学C
    1. 平面上のベクトル
      1. ベクトルの平行、分解
        1. ベクトルの平行条件
        2. ベクトルの分解
      2. ベクトルの相当、大きさ
      3. 点の座標とベクトルの成分
      4. 内積の定義、内積と成分
        1. 内積の定義：
        2. 内積と成分
        3. 内積と平行・垂直条件
      5. 位置ベクトルと共線条件
        1. 分点の位置ベクトル
        2. 共線条件
      6. ベクトル方程式
        1. 直線のベクトル方程式
        2. 内積による直線のベクトル方程式
        3. 平面上の点の存在範囲
        4. 円のベクトル方程式
        5. ベクトルの応用
    2. 空間のベクトル
      1. ベクトルの演算、相当、大きさ
        1. ベクトルの分解
        2. 相当、大きさ
        3. \( \overrightarrow{AB} \) の成分と大きさ
      2. ベクトルの内積
      3. ベクトルの応用
        1. 同じ平面上にある条件
        2. 球面の方程式
      4. (参考) 平面・直線の方程式
        1. 平面の方程式
        2. 直線の方程式
      5. 複素数平面
        1. 絶対値と2点間の距離
      6. 複素数の極形式
        1. 複素数の乗法、除法
      7. 複素数の乗法と回転

数学III

関数

分数関数・無理関数

分数関数 \(\displaystyle \quad y = \dfrac{ax + b}{cx + d} \)

\( \displaystyle y = \dfrac{k}{x\ -\ p} + q \) の形に変形する。
漸近線が２直線 \( x = p, y = q \) の直角双曲線。
\( \displaystyle y = \dfrac{k}{x} \) のグラフを \( x \) 軸方向に \( p \)、 \( y \) 軸方向に \( q \) だけ平行移動したグラフ。

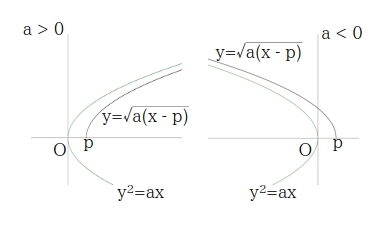
無理関数 \( \quad y = \sqrt{ax + b} \)

\( y = \sqrt{ a(x\ -\ p) } \) の形に変形する。
軸が \( x \) 軸、頂点が原点の放物線 \( y^2 = ax \) の \( y \geqq 0 \) の部分である \( y = \sqrt{ax} \) のグラフを \( x \) 軸方向に \( \displaystyle p =\ – \dfrac{b}{a} \) だけ平行移動したグラフ。

逆関数・合成関数

逆関数
  • \( y = f(x) \quad \Longleftrightarrow \quad x = g(y) \quad \) のとき \( \quad g(x) = f^{-1}(x) \)
  • \( y = f(x) \quad \) と \( \quad y = f^{-1}(x) \quad \) のグラフは、直線 \( \quad y = x \quad \) に関して対称。
  • \( f(x)\ \) の定義域[値域] \(\ =\ f^{-1} (x)\ \) の値域[定義域]
  • 分数関数 \( \displaystyle y = \dfrac{ax + b}{cx + d} \) が逆関数を持つ条件は \( \quad ad\ -\ bc \neq 0 \)
合成関数
  • \( (f \circ g)(x) = g( f(x) ) \)
  • \( (f \circ g)(x) \) と \( (g \circ f)(x) \) は、一般には一致しない。

極限

数列の極限

数列の極限
・収束 \(\displaystyle \lim_{n\to \infty} a_n = \alpha \) (極限値)
}
 極限がある
・発散
{
 \(\displaystyle \lim_{n\to \infty} a_n = \infty \)
\(\displaystyle \lim_{n\to \infty} a_n = – \infty \)
数列は振動する 極限がない
無限等比数列の極限

\( n \ \longrightarrow \ \infty \quad \) のとき \(\ \{ r^n \}\ \) の極限は

\( r \ \gt \ 1\ \) のとき \( r^n \ \longrightarrow \ \infty \) 発散する
\( r \ = \ 1\ \) のとき \( r^n \ \longrightarrow \ 1 \)
}
 \( -1 \ \lt \ r \ \leqq \ 1 \ \) のとき収束する
\( | r | \ \lt \ 1\ \) のとき \( r^n \ \longrightarrow \ 0 \)
\( r \ \leqq \ -1 \ \) のとき 数列は振動する (極限はない)

無限級数

無限級数の収束・発散
  • \(\displaystyle \sum_{n = 1}^{\infty} a_n \) が収束 \(\displaystyle \quad \Longrightarrow \quad \lim_{n\to \infty} a_n \ = \ 0 \)
  • \(\displaystyle \lim_{n\to \infty} a_n \ \neq \ 0 \quad \Longrightarrow \quad \sum_{n = 1}^{\infty} a_n \ \) は発散
無限等比級数 \(\displaystyle \quad \sum_{n = 1}^\infty ar^{n – 1},\ a \neq 0 \)
\( | r | \ \lt \ 1 \ \) のとき 収束して、和は \(\displaystyle \dfrac{a}{1 \ – \ r} \)
\(\displaystyle \qquad S_n = \sum_{k=1}^n ar^{n-1} = \dfrac{a(1\ -\ r^n)}{1\ -\ r} \) \( = \dfrac{a}{1\ -\ r} \ – \ \dfrac{ar^n}{1\ -\ r} \quad \Longrightarrow \quad \lim_{n\to \infty}S_n = \dfrac{a}{1\ -\ r} \ – \ \dfrac{a \cdot 0}{1\ -\ r} \ = \ \dfrac{a}{1\ -\ r} \)
\( | r | \ \geqq \ 1 \ \) のとき 発散する

関数の極限

関数の極限
関数の極限
{
 １つの有限な値 (極限値)
}
 極限がある
\( \infty \) (正の無限大に発散)
\( – \infty \) (負の無限大に発散)
極限はない
右側極限
\(\displaystyle \lim_{x\to a + 0} f(x) \qquad \) [ \( x \gt a \) で \( x \to a \) ]
左側極限
\(\displaystyle \lim_{x\to a – 0} f(x) \qquad \) [ \( x \lt a \) で \( x \to a \) ]

特に \( a = 0 \) なら \(\displaystyle \lim_{x\to +0} f(x), \ \lim_{x\to -0} f(x) \) と表す。

極限に関する性質

\( x \to a \ \) のとき、\( f(x) \to \alpha,\ \ g(x) \to \beta \ \) ならば

  • \(\displaystyle f(x) g(x) \to \alpha \beta,\ \ \dfrac{f(x)}{g(x)} \to \dfrac{\alpha}{\beta}\ \ (\beta \neq 0)\)
  • はさみうちの原理 \(\quad f(x) \leqq h(x) \leqq g(x),\ \ \alpha\ =\ \beta\ \ \) ならば \(\ h(x)\ =\ \alpha \)

[\( x \to a\ \ \) を \(\ \ x \to \infty,\ \ x \to – \infty\ \ \) としても、上で示した性質は成立する。]

三角関数の極限

\(\displaystyle \lim_{x \to 0}{\dfrac{\sin{x}}{x}}\ =\ 1,\quad \lim_{x \to 0}{\dfrac{x}{\sin{x}}}\ =\ 1,\quad \lim_{x \to 0}{\dfrac{\tan{x}}{x}}\ =\ 1 \)
(角の単位は弧度法)

関数の連続・不連続

関数 \( f(x) \) が

  • \( x = a \) で連続とは
    極限値 \(\displaystyle\ \lim_{x \to a}{f(x)}\ \) が存在して \(\displaystyle\ \lim_{x \to a}{f(x)}\ =\ f(a)\ \)
  • \( x = a \) で不連続とは次のいずれかの場合
    • \(\displaystyle \lim_{x \to a}{f(x)}\ \) が極限値を持たない
    • 極限値 \(\displaystyle \lim_{x \to a}{f(x)}\ \) が存在して \(\displaystyle \lim_{x \to a}{f(x)}\ \neq\ f(a) \)
中間値の定理

関数 \(\ f(x)\ \) が閉区間 \([a,\ b]\ \) で連続で \(\ f(a)\ \neq\ f(b)\ \) ならば、\( f(a)\ \) と \(\ f(b)\ \) の間の任意の値 \(\ k\ \) に対して \(\ f(c)\ =\ k\ \) を満たす実数 \(\ c\ \) が、 \(\ a\ \) と \(\ b\ \) の間に少なくとも１つある。

微分法

微分法の基本

微分係数

\(\displaystyle f'(a) = \lim_{h\to 0} \dfrac{f(a + h)\ -\ f(a)}{h} = \lim_{x\to a} \dfrac{f(x)\ -\ f(a)}{x\ -\ a} \)

微分可能と連続、導関数の公式

  • \( f(x) \) が \( x = a \) で微分可能なら連続。
    ただし、逆 (連続なら微分可能) は成立しない。
  • 導関数の定義 \(\displaystyle \qquad f'(x) = \lim_{h\to 0} \dfrac{f(x + h)\ -\ f(x)}{h}\)
  • \( u, v \) は \( x \) の関数で微分可能とする。
    \( (uv)’\ =\ u’v + uv’ \)
    \(\displaystyle \left( \dfrac{u}{v} \right)’ = \dfrac{u’v\ -\ uv’}{v^2} \quad \) 特に \(\displaystyle \quad \left( \dfrac{1}{v} \right)’ = -\dfrac{v’}{v^2}\)
  • \( (x^\alpha)’ = \alpha x^{\alpha – 1} \quad \) ( \( \alpha \) は実数で \( x \gt 0 \) )

三角、指数、対数関数の導関数

三角関数の導関数

\(\displaystyle ( \sin{x} )’ = \cos{x} \)
\(\displaystyle ( \cos{x} )’ = -\sin{x} \)
\(\displaystyle ( \tan{x} )’ = \dfrac{1}{\cos^2{x}} \)

指数・対数関数の導関数

\( a \gt 0,\ a \neq 1 \) とする。

  • \(\displaystyle \lim_{h \to 0} (1 + h)^{\frac{1}{h}} = \lim_{x \to \pm \infty} \left( 1 + \frac{1}{x} \right)^x = e \quad (e = 2.71828) \)
  • \( (e^x)’ = e^x,\quad (a^x)’ = a^x \log_a \)
    \( (\log |x|)’ = \dfrac{1}{x},\quad (\log_a |x|)’ = \dfrac{1}{x \log_{} a}\)
対数微分法

\( y = f(x) \) の両辺の絶対値の自然対数をとって、両辺を微分する。

微分法の応用

積分法

積分法の応用

数学C

平面上のベクトル

ベクトルの平行、分解

ベクトルの平行条件

\(\overrightarrow{\mathstrut a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0} \quad \) のとき
\(\overrightarrow{\mathstrut a}\ /\!/\ \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{b} = k \overrightarrow{a} \quad \) となる \( k \) がある。

ベクトルの分解

\( \overrightarrow{a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0},\quad \overrightarrow{a}\ /\!/\!\!\!\!\backslash\ \overrightarrow{b} \quad \) のとき、任意のベクトル \( \overrightarrow{p} \) は、実数 \( s, t \) を用いてだた１通りに \( \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b} \) の形に表される。

ベクトルの相当、大きさ

\( \overrightarrow{a} = (a_1,\ a_2),\quad \overrightarrow{b} = (b_1,\ b_2)\quad \) とする。

相当：
\( \overrightarrow{a}\ = \overrightarrow{b}\quad \Longleftrightarrow \quad a_1\ =\ b_1,\ a_2\ =\ b_2 \)
大きさ：
\( | \overrightarrow{a} |\ = \sqrt{ {a_1}^2 + {a_2}^2 } \)

点の座標とベクトルの成分

\( A (a_1,\ a_2),\ B (b_1,\ b_2)\quad \) のとき
\(\qquad \overrightarrow{AB}\ =\ (b_1\ -\ a_1,\ b_2\ -\ a_2) \)
\(\qquad |\overrightarrow{AB}|\ =\ \sqrt{ (b_1\ -\ a_1)^2\ +\ (b_2\ -\ a_2)^2 } \)

内積の定義、内積と成分

\( \overrightarrow{a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0} \quad \) とする。

内積の定義：

\( \overrightarrow{a} \) と \( \overrightarrow{b} \) のなす角を \( \theta\quad (0^\circ \leqq \theta \leqq 180^\circ )\quad \) とすると
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}|\ |\overrightarrow{b}|\ \cos \theta \)

内積と成分

\( \overrightarrow{a}\ =\ (a_1,\ a_2),\quad \overrightarrow{b}\ =\ (b_1,\ b_2)\quad \) のとき
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b}\ =\ a_1 b_1\ +\ a_2 b_2 \)
また、\( \ \overrightarrow{a}\ \) と \( \ \overrightarrow{b}\ \) のなす角を \( \theta \) とすると
\(\displaystyle \qquad cos \theta\ =\ \dfrac{ \overrightarrow{a} \cdot \overrightarrow{b} }{ |\overrightarrow{a}|\ |\overrightarrow{b}| }\ =\ \dfrac{ a_1 b_1\ +\ a_2 b_2 }{ \sqrt{ {a_1}^2\ +\ {a_2}^2 }\ \sqrt{ {b_1}^2\ +\ {b_2}^2 } } \)

内積と平行・垂直条件

\( \overrightarrow{a}\ =\ (a_1,\ a_2)\ \neq\ \overrightarrow{0},\quad \overrightarrow{b}\ =\ (b_1,\ b_2)\ \neq\ \overrightarrow{0}\ \) とする。

平行条件
\( \overrightarrow{a}\ // \overrightarrow{b}\quad \Longleftrightarrow\quad \overrightarrow{a}\ \cdot \overrightarrow{b}\ =\pm |\ \overrightarrow{a}\ |\ |\ \overrightarrow{b}\ |\quad \Longleftrightarrow\quad a_1 b_2\ -\ a_2 b_1\ =\ 0 \)
垂直条件
\( \overrightarrow{a}\ \perp\ \overrightarrow{b}\quad \Longleftrightarrow\quad \overrightarrow{a}\ \cdot \overrightarrow{b}\ =\ 0\quad \Longleftrightarrow\quad a_1 b_1\ +\ a_2 b_2\ =\ 0 \)

位置ベクトルと共線条件

分点の位置ベクトル

2点 \( A (\overrightarrow{a}), B (\overrightarrow{b}) \) に対して、線分 \( AB \) を \( m : n \) に分ける点の位置ベクトル。

内分
\(\displaystyle \dfrac{ n \overrightarrow{a} + m \overrightarrow{b} }{ m + n} \)
外分
\(\displaystyle \dfrac{ -\ n \overrightarrow{a} + m \overrightarrow{b} }{ m\ -\ n} \)
共線条件

2点 \( A, B \) が異なるとき
点 \( P \) が直線 \( AB \) 上にある \( \quad \Longleftrightarrow \quad \overrightarrow{AP} = k \overrightarrow{AB} \) となる実数 \( k \) がある

ベクトル方程式

直線上の任意の点 \( P \) の位置ベクトルを \( \overrightarrow{p} \) とし、\( s, t \) を実数の変数とする。

直線のベクトル方程式

  1. 点 \( A ( \overrightarrow{a} ) \) を通り、\( \overrightarrow{d} (\neq \overrightarrow{0} ) \) に平行な直線のベクトル方程式
    \( \qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d} \)
  2. 異なる2点 \( A (\overrightarrow{a}),\ B (\overrightarrow{b}) \) を通る直線のベクトル方程式
    \( \qquad \overrightarrow{p} = (1\ -\ t) \overrightarrow{a} + t \overrightarrow{b} \qquad \) または
    \( \qquad \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b}, \quad s + t = 1 \)

内積による直線のベクトル方程式

点 \( A (\overrightarrow{a} ) \) を通り、\( \overrightarrow{n} (\neq \overrightarrow{0}) \) に垂直な直線のベクトル方程式
\( \qquad \overrightarrow{n} \cdot ( \overrightarrow{p}\ -\ \overrightarrow{a} ) = 0 \)

平面上の点の存在範囲

\( \triangle OAB \) に対して、\( \overrightarrow{OP} = s \overrightarrow{OA} + t \overrightarrow{OB} \) のとき、点 \( P \) の存在範囲は

  1. 直線 \( AB \quad \Longleftrightarrow \quad s + t = 1 \)
    特に 線分 \( AB \quad \Longleftrightarrow \quad s + t = 1,\; s \geqq 0,\; t \geqq 0 \)
  2. \( \triangle OAB \) の周と内部 \( \quad \Longleftrightarrow \quad 0 \leqq s + t \leqq 1,\; s \geqq 0,\; t \geqq 0 \)
  3. 平行四辺形 \( OACB \) の周と内部 \( \quad \Longleftrightarrow \quad 0 \leqq s \leqq 1,\; 0 \leqq t \leqq 1 \)

円のベクトル方程式

中心 \( C (\overrightarrow{c}) \)、半径 \( r \) の円のベクトル方程式
\( \qquad |\ \overrightarrow{p}\ -\ \overrightarrow{c}\ | = r \)

ベクトルの応用

点 \( P \) が直線 \( AB \) 上にある \( \quad \Longleftrightarrow \quad \overrightarrow{OP} = s \overrightarrow{OA} + t \overrightarrow{OB},\; s + t = 1 \) となる実数 \( s,\; t \) がある。

空間のベクトル

ベクトルの演算、相当、大きさ

ベクトルの分解

同じ平面上にない4点 \( O, A, B, C \) に対して \( \overrightarrow{OA} = \overrightarrow{a},\ \overrightarrow{OB} = \overrightarrow{b},\ \overrightarrow{OC} = \overrightarrow{c}\ \) とすると、任意のベクトル \(\ \overrightarrow{p}\ \) は実数 \(\ s, t, u\ \) を用いてただ一通りに \(\ \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b} + u \overrightarrow{c}\ \) の形に表される。

相当、大きさ

\( \overrightarrow{a}\ =\ (a_1,\ a_2,\ a_3),\ \overrightarrow{b}\ =\ (b_1,\ b_2,\ b_3)\ \) とする。
\( \qquad \overrightarrow{a}\ =\ \overrightarrow{b} \qquad \Longleftrightarrow \qquad a_1 = b_1,\ a_2 = b_2,\ a_3 = b_3 \)
\( \qquad |\overrightarrow{a}|\ =\ \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\)

\( \overrightarrow{AB} \) の成分と大きさ

\( A (a_1,\ a_2,\ a_3),\ B (b_1,\ b_2,\ b_3)\ \) のとき
\( \qquad \overrightarrow{AB}\ =\ ( b_1 – a_1,\ b_2 – a_2,\ b_3 – a_3 ) \)
\( \qquad |\overrightarrow{AB}|\ =\ \sqrt{(b_1 – a_1)^2 + (b_2 – a_2)^2 + (b_3 – a_3)^2 } \)

ベクトルの内積

\( \overrightarrow{a}\ =\ (a_1,\ a_2,\ a_3),\ \overrightarrow{b}\ =\ (b_1,\ b_2,\ b_3)\ \) のとき
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b}\ =\ a_1 b_1\ +\ a_2 b_2\ +\ a_3 b_3 \)

ベクトルの応用

同じ平面上にある条件

\( s, t, u \) を実数とする。
点 \( P ( \overrightarrow{p} ) \) が3点 \( A ( \overrightarrow{a} ),\ B ( \overrightarrow{b} ),\ C ( \overrightarrow{c} )\ \) の定める平面上にある
\( \qquad \Longleftrightarrow \quad \overrightarrow{CP}\ =\ s \overrightarrow{CA} + t \overrightarrow{CB} \)
\( \qquad \Longleftrightarrow \quad \overrightarrow{p}\ =\ s \overrightarrow{a} + t \overrightarrow{b} + u \overrightarrow{c}, \qquad s + t + u = 1 \)

球面の方程式
  • 点 \( (a, b, c) \) を中心とする 半径 \( r \) の球面
    \( \qquad (x\ -\ a)^2\ +\ (y\ -\ b)^2\ +\ (z\ -\ c)^2\ =\ r^2 \)
    特に、原点を中心とする 半径 \( r \) の球面
    \( \qquad x^2\ +\ y^2\ +\ z^2\ =\ r^2 \)
  • 一般形 \(\qquad x^2\ +\ y^2\ +\ z^2\ +\ Ax\ +\ By\ +\ Cz\ +\ D\ =\ 0 \)
    ただし、\(\qquad A^2\ +\ B^2\ +\ C^2\ -\ 4D\ \gt\ 0 \)
  • 中心が \(\ C(\overrightarrow{c})\ \)、半径が \( r \) の球面ベクトル方程式 \( \qquad | \overrightarrow{p}\ -\ \overrightarrow{c} |\ =\ r\)

(参考) 平面・直線の方程式

平面の方程式

  • 点 \( A ( \overrightarrow{a} ) \) を通り、\( n (\neq 0 ) \) に垂直な平面のベクトル方程式 \( \qquad \overrightarrow{n} \cdot (\overrightarrow{p}\ -\ \overrightarrow{a})\ =\ 0 \)
  • \( A (x_1,\ y_1,\ z_1),\ \overrightarrow{n}\ =\ (a,\ b,\ c) \) のとき、平面の方程式 \( \qquad a (x\ -\ x_1)\ +\ b (y\ -\ y_1)\ +\ c (z\ -\ z_1)\ =\ 0 \)
  • 平面の方程式の一般形 \(\qquad ax\ +\ by\ +\ cz\ + d\ =\ 0 \)
直線の方程式

\( t \) を実数とする。

  • 点 \( A (\overrightarrow{a} ) \) を通り、\( \overrightarrow{d} (\neq \overrightarrow{0}) \) に平行な直線ベクトル方程式 \( \qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d}\)
  • \( A (x_1,\ y_1,\ z_1),\ \overrightarrow{d} = (l,\ m,\ n) \) のとき、直線の方程式
    1. \( x\ =\ x_1\ +\ lt,\ y\ =\ y_1\ +\ mt,\ z\ =\ z_1\ +\ nt \)
    2. \(\displaystyle \dfrac{ x\ -\ x_1 }{l}\ =\ \dfrac{ y\ -\ y_1 }{m}\ =\ \dfrac{ z\ -\ z_1 }{n} \qquad (lmn\ \neq\ 0) \)

複素数平面複素数平面

絶対値と2点間の距離
定義
\( z = a + b i\ \) に対し \(\ |z|\ =\ \sqrt{a^2 + b^2} \)
絶対値の性質
\( z,\ \alpha,\ \beta \) は複素数とする。
\( \qquad |z|\ =\ 0 \quad \Longleftrightarrow \quad z\ =\ 0 \)
\( \qquad |z|\ =\ |-z|\ =\ |\bar{z}|,\ z \bar{z}\ =\ |z|^2 \)
\( \qquad |\alpha \beta|\ =\ |\alpha| |\beta|\)
\(\displaystyle \qquad \left| \dfrac{\alpha}{\beta} \right|\ =\ \dfrac{|\alpha|}{|\beta|} \qquad (\beta\ \neq\ 0) \)
2点 \(\ \alpha,\ \beta\ \) 間の距離
\( | \beta\ -\ \alpha | \)

複素数の極形式

複素数平面上で、\(\ O(0),\ P(z),\ z\ =\ a\ +\ bi\ \ (\neq\ 0),\ OP\ =\ r,\ OP\) と実軸の正の部分とのなす角が \(\ \theta\ \) のとき、
\( \qquad z\ =\ r (\cos{\theta}\ + i \sin{\theta}) \quad (r\ \gt\ 0) \)

複素数の乗法、除法

\( z_1\ =\ r_1 (\cos{\theta_1}\ + i \sin{\theta_1}),\ z_2\ =\ r_2 (\cos{\theta_2}\ + i \sin{\theta_2})\ \) とする。

複素数 \(\ z_1,\ z_2\ \) の乗法
\( z_1 z_2\ =\ r_1 r_2 \{ cos( \theta_1\ +\ \theta_2 )\ +\ i \sin( \theta_1\ +\ \theta_2 ) \} \)
\( \qquad |z_1 z_2|\ =\ |z_1| |z_2|, \quad arg\ z_1 z_2\ =\ arg\ z_1\ +\ arg\ z_2 \)
複素数 \(\ z_1,\ z_2\ \) の除法 ( \( z_2\ \neq\ 0\ \) とする)
\( \displaystyle \dfrac{z_1}{z_2}\ =\ \dfrac{r_1}{r_2} \{ cos( \theta_1\ -\ \theta_2 )\ +\ i \sin( \theta_1\ -\ \theta_2 ) \} \)
\( \displaystyle \qquad \left| \dfrac{z_1}{z_2} \right|\ =\ \dfrac{|z_1|}{|z_2|}, \quad arg \dfrac{z_1}{z_2}\ =\ arg\ z_1\ -\ arg\ z_2 \)

複素数の乗法と回転

\( P(z),\ r\ \gt\ 0\ \) とする。
点 \(\ r ( \cos{\theta}\ +\ \sin{\theta} ) \cdot z\ \) は、点 \( P \) を原点を中心として角 \( \theta \) だけ回転し、原点からの距離を \( r \) 倍した点である。

式と曲線

ホーム
トップ
PAGE TOP