数学III・C
 数学III・C
数学III・C- 数学III
- 数学C
- 平面上のベクトル
- 空間のベクトル
- 複素数平面
- 式と曲線
- 2次曲線
- 放物線 \(\qquad y^2 = 4px \quad (p \neq 0) \qquad \) [標準形]
- 楕円 \(\displaystyle \qquad \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \quad (a \gt b \gt 0) \qquad \) [標準形]
- 双曲線 \(\displaystyle \qquad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2} = 1 \quad ( a \gt 0,\ b \gt 0) \qquad \) [標準形]
- 2次曲線の接線
- 離心率 \( e \) と準線 \( l \)
- 媒介変数表示
- 極座標と極方程式
- 2次曲線
数学III
関数
分数関数・無理関数
分数関数 \(\displaystyle \quad y = \dfrac{ax + b}{cx + d} \)
\( \displaystyle y = \dfrac{k}{x\ -\ p} + q \) の形に変形する。
漸近線が2直線 \( x = p, y = q \) の直角双曲線。
\( \displaystyle y = \dfrac{k}{x} \) のグラフを \( x \) 軸方向に \( p \)、 \( y \) 軸方向に \( q \) だけ平行移動したグラフ。
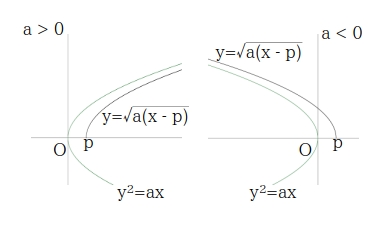
無理関数 \( \quad y = \sqrt{ax + b} \)
\( y = \sqrt{ a(x\ -\ p) } \) の形に変形する。
軸が \( x \) 軸、頂点が原点の放物線 \( y^2 = ax \) の \( y \geqq 0 \) の部分である \( y = \sqrt{ax} \) のグラフを \( x \) 軸方向に \( \displaystyle p =\ – \dfrac{b}{a} \) だけ平行移動したグラフ。
逆関数・合成関数
逆関数
- \( y = f(x) \quad \Longleftrightarrow \quad x = g(y) \quad \) のとき \( \quad g(x) = f^{-1}(x) \)
- \( y = f(x) \quad \) と \( \quad y = f^{-1}(x) \quad \) のグラフは、直線 \( \quad y = x \quad \) に関して対称。
- \( f(x)\ \) の定義域[値域] \(\ =\ f^{-1} (x)\ \) の値域[定義域]
- 分数関数 \( \displaystyle y = \dfrac{ax + b}{cx + d} \) が逆関数を持つ条件は \( \quad ad\ -\ bc \neq 0 \)
合成関数
- \( (f \circ g)(x) = g( f(x) ) \)
- \( (f \circ g)(x) \) と \( (g \circ f)(x) \) は、一般には一致しない。
極限
数列の極限
数列の極限
| ・収束 | \(\displaystyle \lim_{n\to \infty} a_n = \alpha \) (極限値) |
}
|
極限がある | |
| ・発散 |
{
|
\(\displaystyle \lim_{n\to \infty} a_n = \infty \) | ||
| \(\displaystyle \lim_{n\to \infty} a_n = – \infty \) | ||||
| 数列は振動する | 極限がない |
無限等比数列の極限
\( n \ \longrightarrow \ \infty \quad \) のとき \(\ \{ r^n \}\ \) の極限は
| \( r \ \gt \ 1\ \) のとき | \( r^n \ \longrightarrow \ \infty \) | 発散する | ||
| \( r \ = \ 1\ \) のとき | \( r^n \ \longrightarrow \ 1 \) |
}
|
\( -1 \ \lt \ r \ \leqq \ 1 \ \) のとき収束する | |
| \( | r | \ \lt \ 1\ \) のとき | \( r^n \ \longrightarrow \ 0 \) | |||
| \( r \ \leqq \ -1 \ \) のとき | 数列は振動する (極限はない) | |||
| \( | r | \ \lt \ 1 \ \) のとき | 収束して、和は \(\displaystyle \dfrac{a}{1 \ – \ r} \) \(\displaystyle \qquad S_n = \sum_{k=1}^n ar^{n-1} = \dfrac{a(1\ -\ r^n)}{1\ -\ r} \) \( = \dfrac{a}{1\ -\ r} \ – \ \dfrac{ar^n}{1\ -\ r} \quad \Longrightarrow \quad \lim_{n\to \infty}S_n = \dfrac{a}{1\ -\ r} \ – \ \dfrac{a \cdot 0}{1\ -\ r} \ = \ \dfrac{a}{1\ -\ r} \) |
| \( | r | \ \geqq \ 1 \ \) のとき | 発散する |
関数の極限
関数の極限
| 関数の極限 |
{
|
1つの有限な値 (極限値) |
}
|
極限がある |
| \( \infty \) (正の無限大に発散) | ||||
| \( – \infty \) (負の無限大に発散) | ||||
| 極限はない | ||||
- 右側極限
- \(\displaystyle \lim_{x\to a + 0} f(x) \qquad \) [ \( x \gt a \) で \( x \to a \) ]
- 左側極限
- \(\displaystyle \lim_{x\to a – 0} f(x) \qquad \) [ \( x \lt a \) で \( x \to a \) ]
特に \( a = 0 \) なら \(\displaystyle \lim_{x\to +0} f(x), \ \lim_{x\to -0} f(x) \) と表す。
極限に関する性質
\( x \to a \ \) のとき、\( f(x) \to \alpha,\ \ g(x) \to \beta \ \) ならば
- \(\displaystyle f(x) g(x) \to \alpha \beta,\ \ \dfrac{f(x)}{g(x)} \to \dfrac{\alpha}{\beta}\ \ (\beta \neq 0)\)
- はさみうちの原理 \(\quad f(x) \leqq h(x) \leqq g(x),\ \ \alpha\ =\ \beta\ \ \) ならば \(\ h(x)\ =\ \alpha \)
[\( x \to a\ \ \) を \(\ \ x \to \infty,\ \ x \to – \infty\ \ \) としても、上で示した性質は成立する。]
三角関数の極限
\(\displaystyle \lim_{x \to 0}{\dfrac{\sin{x}}{x}}\ =\ 1,\quad \lim_{x \to 0}{\dfrac{x}{\sin{x}}}\ =\ 1,\quad \lim_{x \to 0}{\dfrac{\tan{x}}{x}}\ =\ 1 \)
(角の単位は弧度法)
関数の連続・不連続
関数 \( f(x) \) が
- \( x = a \) で連続とは
極限値 \(\displaystyle\ \lim_{x \to a}{f(x)}\ \) が存在して \(\displaystyle\ \lim_{x \to a}{f(x)}\ =\ f(a)\ \) - \( x = a \) で不連続とは次のいずれかの場合
- \(\displaystyle \lim_{x \to a}{f(x)}\ \) が極限値を持たない
- 極限値 \(\displaystyle \lim_{x \to a}{f(x)}\ \) が存在して \(\displaystyle \lim_{x \to a}{f(x)}\ \neq\ f(a) \)
中間値の定理
関数 \(\ f(x)\ \) が閉区間 \([a,\ b]\ \) で連続で \(\ f(a)\ \neq\ f(b)\ \) ならば、\( f(a)\ \) と \(\ f(b)\ \) の間の任意の値 \(\ k\ \) に対して \(\ f(c)\ =\ k\ \) を満たす実数 \(\ c\ \) が、 \(\ a\ \) と \(\ b\ \) の間に少なくとも1つある。
微分法
微分法の基本
微分係数
\(\displaystyle f'(a) = \lim_{h\to 0} \dfrac{f(a + h)\ -\ f(a)}{h} = \lim_{x\to a} \dfrac{f(x)\ -\ f(a)}{x\ -\ a} \)
微分可能と連続、導関数の公式
- \( f(x) \) が \( x = a \) で微分可能なら連続。
ただし、逆 (連続なら微分可能) は成立しない。 - 導関数の定義 \(\displaystyle \qquad f'(x) = \lim_{h\to 0} \dfrac{f(x + h)\ -\ f(x)}{h}\)
- \( u, v \) は \( x \) の関数で微分可能とする。
\( (uv)’\ =\ u’v + uv’ \)
\(\displaystyle \left( \dfrac{u}{v} \right)’ = \dfrac{u’v\ -\ uv’}{v^2} \quad \) 特に \(\displaystyle \quad \left( \dfrac{1}{v} \right)’ = -\dfrac{v’}{v^2}\) - \( (x^\alpha)’ = \alpha x^{\alpha – 1} \quad \) ( \( \alpha \) は実数で \( x \gt 0 \) )
三角、指数、対数関数の導関数
三角関数の導関数
\(\displaystyle ( \sin{x} )’ = \cos{x} \)
\(\displaystyle ( \cos{x} )’ = -\sin{x} \)
\(\displaystyle ( \tan{x} )’ = \dfrac{1}{\cos^2{x}} \)
指数・対数関数の導関数
\( a \gt 0,\ a \neq 1 \) とする。
- \(\displaystyle \lim_{h \to 0} (1 + h)^{\frac{1}{h}} = \lim_{x \to \pm \infty} \left( 1 + \frac{1}{x} \right)^x = e \quad (e = 2.71828) \)
- \( (e^x)’ = e^x,\quad (a^x)’ = a^x \log {a} \)
\( (\log |x|)’ = \dfrac{1}{x},\quad (\log_a |x|)’ = \dfrac{1}{x \log {a} }\)
対数微分法
\( y = f(x) \) の両辺の絶対値の自然対数をとって、両辺を微分する。
高次導関数、関数のいろいろな表し方と導関数
高次導関数
- \( f^{\prime}(x) \) の導関数が 第2次導関数 \( f^{\prime\prime}(x) \)、\( f^{\prime\prime}(x) \) の導関数が 第3次導関数 \( f^{\prime\prime\prime}(x) \)
- \( y = f(x) \) を \( n \) 回続けて微分して得られる関数を第 \( n \) 次導関数と言い
\(\displaystyle \qquad y^{\prime}{(n)}, \quad \dfrac{d^n y}{dx^n}, \quad f^{(n)}\)
などと表す。
方程式 \( F(x, y) = 0 \) で表された関数の導関数
- \( y \) が \( x \) の関数のとき \(\displaystyle \qquad \dfrac{d}{dx} f(y) = \dfrac{d}{dy} f(y) \cdot \dfrac{dy}{dx} \)
- \( F(x, y) = 0 \) であらわされた \( x \) の関数 \( y \) の導関数を求めるには \( F(x, y) = 0 \) の両辺を \( x \) で微分する。このとき、1 の公式を利用する。
媒介変数で表された関数の導関数
\( x = f(t),\ y = g(t)\ \) が微分可能で \(\ f^{\prime}(t) \neq 0\ \) のとき、\(\ x = f(t)\ \) の逆関数 \(\ t = f^{-1}(x)\ \) があれば、\(\ y = g( f^{-1}( x ) )\ \) を合成関数と逆関数の微分法を用いて次のように微分できる。
\(\displaystyle \begin{eqnarray} \qquad
\dfrac{dy}{dx} &=& \dfrac{dy}{dt}\cdot\dfrac{dt}{dx} \qquad \qquad &\ & (合成関数の微分法) \\
&=& \dfrac{dy}{dt} \cdot \dfrac{1}{ \dfrac{dx}{dt} } &\ & (逆関数の微分法) \\
\end{eqnarray} \)
\( \qquad \therefore \dfrac{dy}{dx} = \dfrac{ \dfrac{dy}{dt} }{ \dfrac{dx}{dt} } \)
第2次導関数は
\(\displaystyle \begin{eqnarray} \qquad
\dfrac{d^2y}{dx^2} &=& \dfrac{d}{dx} \left( \dfrac{dy}{dx} \right) \qquad \qquad & & (定義) \\
&=& \dfrac{d}{dt}\left( \dfrac{dy}{dx} \right) \cdot \dfrac{dt}{dx} & & (合成関数の微分法) \\
&=& \dfrac{ \dfrac{d}{dt}\left( \dfrac{dy}{dx} \right) }{ \dfrac{dx}{dt} } & & (逆関数の微分法)
\end{eqnarray} \)
という手順で計算できる。
微分法の応用
接線と法線
接線と法線の方程式
曲線 \(\ y = f(x)\ \) 上の点 \(\ A(a,\ f(a))\ \) における
- 接線の方程式は \(\quad y\ -\ f(a)\ =\ f^{\prime}(a) (x\ -\ a) \)
- 法線の方程式は \(\quad f^{\prime}(a) \neq 0\ \) のとき
\(\displaystyle \qquad y\ -\ f(a)\ =\ – \dfrac{1}{f^{\prime}(a)} (x\ -\ a) \)
平均値の定理
ロルの定理
関数 \( f(x) \) が区間 \(\ [a,\ b]\ \) で連続、区間 \(\ (a,\ b)\ \) で微分可能で、\( f(a) = f(b)\ \) ならば \(\ f^{\prime}(c) = 0,\ \ a \lt c \lt b\ \) を満たす実数 \(\ c\ \) が存在する。
平均値の定理
関数 \( f(x) \) が区間 \(\ [a,\ b]\ \) で連続、区間 \(\ (a,\ b)\ \) で微分可能ならば
\(\displaystyle \qquad \dfrac{f(b)\ -\ f(a)}{b\ -\ a}\ =\ f^{\prime}(c),\ \ a \lt c \lt b\ \)
を満たす実数 \(\ c\ \) が存在する。
関数の増減と極値
関数の増減
関数 \(\ f(x)\ \) が区間 \(\ [a,\ b]\ \) で連続、区間 \(\ (a,\ b)\ \) で微分可能であるとき
区間 \(\ (a,\ b)\ \) で
- 常に \(\ f^{\prime}(x)\ \gt\ 0\ \) ならば区間 \(\ [a,\ b]\ \) で単調に増加
- 常に \(\ f^{\prime}(x)\ \lt\ 0\ \) ならば区間 \(\ [a,\ b]\ \) で単調に減少
- 常に \(\ f^{\prime}(x)\ = 0\ \) ならば区間 \(\ [a,\ b]\ \) で定数
関数の極大・極小
- \( x = a \) を含む十分小さい開区間において
- \(\ x\ \neq\ a\ \) なら \(\ f(x)\ \lt\ f(a)\ \) のとき \(\ f(x)\ \) は \(\ x\ =\ a\ \) で極大
- \(\ x\ \neq\ a\ \) なら \(\ f(x)\ \gt\ f(a)\ \) のとき \(\ f(x)\ \) は \(\ x\ =\ a\ \) で極小
といい、\(\ f(a)\ \) をそれぞれ極大値、極小値という。
極大値と極小値をまとめて極値という。 - \(\ f(x)\ \) が \( x\ =\ a \) で微分可能であるとき
\(\qquad x\ =\ a\ \) で極値をとる \(\quad \Longrightarrow \quad f^{\prime}(a)\ =\ 0 \qquad \) (逆は不成立)
極値と第2次導関数
\(\ x = a\ \) を含むある区間で \(\ f^{\prime\prime} (x)\ \) は連続とする。
- \( f^{\prime}(a) = 0\ \) かつ \( f^{\prime\prime}(a) \lt 0\ \) ならば \(\ f(a)\ \) は極大値
- \( f^{\prime}(a) = 0\ \) かつ \( f^{\prime\prime}(a) \gt 0\ \) ならば \(\ f(a)\ \) は極小値
曲線 \(\ y = f(x)\ \) の凹凸・変曲点
- ある区間で \(\ f^{\prime\prime}(x) \gt 0 \) ならば、その区間で下に凸
ある区間で \(\ f^{\prime\prime}(x) \lt 0 \) ならば、その区間で上に凸 - 変曲点 \( \qquad \) 凹凸が変わる曲線状の点のこと。
- 点 \(\ (a, f(a))\ \) が曲線 \(\ y\ =\ f(a)\ \) の変曲点ならば
\(\qquad f^{\prime\prime} = 0 \)
方程式・不等式への応用
方程式 \(\ f(x) = g(x)\ \) の実数解の個数
\( y\ =\ f(x)\ \) のグラフと \( y\ =\ g(x)\ \) のグラフの共有点の個数を調べる。
不等式 \(\ f(x) \gt g(x)\ \) の証明
\( F(x)\ =\ f(x)\ -\ g(x)\ \) として、\(\ F(x)\ \) の最小値 \(\ m\ \) を求め、\(\ m\ \gt\ 0 \) を示す。
速度・加速度、近似式
平面上の運動の速度・加速度
平面上の点 \( P \) が曲線を描いて運動し、時刻 \( t \) のときの位置 (座標) が \( t \) の関数 \(\ x = f(t)\ \)、\(\ y = g(t)\ \) で与えられるとき、速度 \(\ \overrightarrow{v}\ \)、加速度 \(\ \overrightarrow{\alpha}\ \) は
\(\displaystyle \qquad \overrightarrow{v} = \left( \dfrac{dx}{dt}, \dfrac{dy}{dt} \right), \qquad \overrightarrow{\alpha} = \left( \dfrac{d^2 x}{ d t^2 }, \dfrac{d^2 y}{ d t^2 } \right) \)
また、速さ \(\ |\overrightarrow{v}|\ \)、加速度 \(\ \overrightarrow{\alpha}\ \) の大きさ \(\ |\overrightarrow{\alpha}|\ \) は、順に
\(\displaystyle \qquad \sqrt{ \left( \dfrac{dx}{dt} \right)^2 + \left( \dfrac{dy}{dt} \right)^2 }, \qquad \sqrt{ \left( \dfrac{d^2x}{dt^2} \right)^2 + \left( \dfrac{d^2y}{dt^2} \right)^2 } \)
1次の近似式
- \( |h|\ \) が十分小さい時 \( \qquad f(a + h) \fallingdotseq f(a) + f^{\prime}(a)h \)
- \( |x|\ \) が十分小さい時 \( \qquad f(x) \fallingdotseq f(0) + f^{\prime}(0)h \)
積分法
不定積分
基本的な関数の不定積分
\( C \) は積分定数とする。
- \(\displaystyle \int{x^\alpha\ dx} = \dfrac{x^{\alpha + 1}}{\alpha + 1} + C \quad \) (\( \alpha \) は実数、\( \alpha \neq -1 \))
\(\displaystyle \int{\dfrac{dx}{x}} = \log{ |x| } + C \) - \(\displaystyle \int{ \sin{x}\ dx} = -\cos{x} + C \)
\(\displaystyle \int{ \cos{x}\ dx} = \sin{x} + C \)
\(\displaystyle \int{ \dfrac{dx}{\cos^2{x}} } = \tan{x} + C \) - \(\displaystyle \int{ e^x\ dx} = e^x + C \)
\(\displaystyle \int{ a^x\ dx } = \dfrac{a^x}{\log{ a }} + C \) - \(\displaystyle \int{ \{f(x)\}^r f^\prime(x)\ dx } = \dfrac{ \{f(x)\}^{r + 1} }{ r + 1 } + C \qquad (r \neq -1) \)
\(\displaystyle \int{ \dfrac{f^\prime (x)}{f(x)}\ dx } = \log{ |f(x)| } + C \)
置換積分法
\( C \) は積分定数とする。
- \(\displaystyle \int{ f( g(x) ) g^{\prime}(x)\ dx } = \int{ f(u)\ du},\ g(x) = u \)
\(\displaystyle \int{ f(x)\ dx } = \int{ f(g(t)) g^{\prime}(t)\ dt },\ x = g(t) \)
特に \(\displaystyle \int{ \dfrac{ f^{\prime}(x) }{ f(x) }\ dx } = \log{ |f(x)| } + C \)
\(\displaystyle \int{ \{f(x)\}^{\alpha} f^{\prime}(x)\ dx } = \dfrac{ \{f(x)\}^{\alpha + 1} }{ \alpha + 1 } + C \quad (\alpha \neq -1) \)
部分積分法
\(\displaystyle \qquad \int{ f(x) g^{\prime}(x)\ dx } = f(x) g(x)\ -\ \int{ f^{\prime}(x) g(x)\ dx } \)
\( \qquad \)特に \(\displaystyle \quad \int{ f(x)\ dx } = xf(x)\ -\ \int{ xf^{\prime}(x)\ dx } \)
定積分
定積分の置換積分法
\(x = g(t),\ a = g(p),\ b = g(q)\quad \) のとき
\(\displaystyle \qquad \int_a^b{ f(x)\ dx } = \int_p^q{ f( g(t) ) g^{\prime}(t)\ dt } \)
定積分の部分積分法
\(\displaystyle \qquad \int_a^b{ f(x) g^{\prime}(x)\ dx } = \Big[ f(x) g(x) \Big]_a^b\ -\ \int_a^b{ f^{\prime}(x) g(x)\ dx } \)
偶関数・奇関数の定積分
\( f(x) \) が
- 偶関数のとき \(\displaystyle \quad \int_{-a}^a{ f(x)\ dx} = 2 \int_0^a{ f(x)\ dx} \)
- 奇関数のとき \(\displaystyle \quad \int_{-a}^a{ f(x)\ dx} = 0 \)
定積分で表された関数
\( a,\ b\ \) は定数とする。
- \(\displaystyle \int_a^b{ f(x,\ t)\ dt } \) は \( t \) に無関係で、\( x \) の関数である。
- \(\displaystyle \dfrac{d}{dx} \int_a^x{ f(t)\ dt = f(x)} \)
\(\displaystyle \dfrac{d}{dx} \int_{h(x)}^{g(x)}{ f(t)\ dt } = f( g(x)) g^{\prime}(x)\ -\ f( h(x) ) h^{\prime}(x) \)
定積分と和の極限(区分求積法)
\( f(x)\ \) が区間 \(\ [a,\ b]\ \) で連続で、この区間を \( n \) 等分して両端と分点を \( a = x_0,\ x_1,\ x_2,\cdots,\ x_n = b \) とし、\(\displaystyle \dfrac{b\ -\ a}{n} = \Delta x \) とおくと
\(\displaystyle \qquad \int_a^b{ f(x)\ dx } = \lim_{n \to \infty}{ \sum_{k = 0}^{n – 1}{ f(x_k) \Delta x }} = \lim_{n \to \infty}{ \sum_{k = 1}^n{ f(x_k) \Delta x } } \)
特に \( a = 0,\ b = 1 \) とすると
\(\displaystyle \qquad \int_0^1{ f(x)\ dx } = \lim_{n \to \infty}{ \dfrac{1}{n} \sum_{k = 0}^{n – 1}{ f\left( \dfrac{k}{n} \right) }} = \lim_{n \to \infty}{ \dfrac{1}{n} \sum_{k = 1}^{n}{ f\left( \dfrac{k}{n} \right) }} \)
積分法の応用
面積、体積、曲線の長さ
曲線 \( x = g(y) \) と \( y \) 軸の間の面積
曲線 \( x = g(y) \) と \( y \) 軸と2直線 \( y = c,\ y = d\ (c \lt d) \) で囲まれた部分の面積
\(\displaystyle \qquad S = \int_c^d{ |g(y)|\ dy } \)
\( x = f(t),\ y = g(t) \) で表される曲線と面積
\(\displaystyle \qquad S = \int_a^b{ y\ dx } = \int_\alpha^\beta{ g(t) f^{\prime}(t)\ dt } \)
\(\qquad\) ただし、常に \( y \geqq 0,\ a = f(\alpha),\ b = f(\beta) \)
立体の体積
切り口の面積が \( S(x) \) の立体の体積は、\( a \lt b \) のとき
\(\displaystyle \qquad \int_a^b{ S(x)\ dx } \)
回転体の体積
曲線 \( y = f(x) \) と \( x \) 軸と2直線 \( x = a,\ x = b\ (a \lt b) \) で囲まれた部分を \( x \) 軸の周りに1回転してできる立体の体積
\(\displaystyle \qquad V = \pi \int_a^b{ \{f(x)\}^2\ dx } = \pi \int_a^b{ y^2\ dx} \)
曲線の長さ
- 曲線 \( \quad x = f(t),\ y = g(t) \quad (\alpha \leqq t \leqq \beta ) \quad \) の長さは
\(\displaystyle \int_\alpha^\beta{ \sqrt{ \left( \dfrac{dx}{dt} \right)^2 + \left( \dfrac{dy}{dt} \right)^2 }\ dt } = \int_\alpha^\beta{ \sqrt{ \{ f^{\prime}(t) \}^2 + \{ g^{\prime}(t) \}^2 }\ dt } \) - 曲線 \( \quad y = f(x) \quad (a \leqq x \leqq b ) \quad \) の長さは
\(\displaystyle \int_a^b{ \sqrt{ 1 + \left( \dfrac{dy}{dx} \right)^2 }\ dx } = \int_a^b{ \sqrt{ 1 + \{ f^{\prime}(x) \}^2 } \ dx } \)
発展事項 (微分方程式)
簡単な微分方程式と一般解
- 変数分離形 \(\displaystyle f(y) \dfrac{dy}{dx} = g(x) \) に変形できるときは、両辺を \( x \) で積分する。\(\displaystyle \int{ f(y)\ dy } = \int{ g(x)\ dx } \)
- \(\displaystyle \dfrac{dy}{dx} = ky \) の一般会は \( y = Ce^{kx}\quad \) ( \( C \) は任意定数)
数学C
平面上のベクトル
ベクトルの平行、分解
ベクトルの平行条件
\(\overrightarrow{\mathstrut a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0} \quad \) のとき
\(\overrightarrow{\mathstrut a}\ /\!/\ \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{b} = k \overrightarrow{a} \quad \) となる \( k \) がある。
ベクトルの分解
\( \overrightarrow{a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0},\quad \overrightarrow{a}\ /\!/\!\!\!\!\backslash\ \overrightarrow{b} \quad \) のとき、任意のベクトル \( \overrightarrow{p} \) は、実数 \( s, t \) を用いてだた1通りに \( \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b} \) の形に表される。
ベクトルの相当、大きさ
\( \overrightarrow{a} = (a_1,\ a_2),\quad \overrightarrow{b} = (b_1,\ b_2)\quad \) とする。
- 相当:
- \( \overrightarrow{a}\ = \overrightarrow{b}\quad \Longleftrightarrow \quad a_1\ =\ b_1,\ a_2\ =\ b_2 \)
- 大きさ:
- \( | \overrightarrow{a} |\ = \sqrt{ {a_1}^2 + {a_2}^2 } \)
点の座標とベクトルの成分
\( A (a_1,\ a_2),\ B (b_1,\ b_2)\quad \) のとき
\(\qquad \overrightarrow{AB}\ =\ (b_1\ -\ a_1,\ b_2\ -\ a_2) \)
\(\qquad |\overrightarrow{AB}|\ =\ \sqrt{ (b_1\ -\ a_1)^2\ +\ (b_2\ -\ a_2)^2 } \)
内積の定義、内積と成分
\( \overrightarrow{a} \neq \overrightarrow{0},\quad \overrightarrow{b} \neq \overrightarrow{0} \quad \) とする。
内積の定義:
\( \overrightarrow{a} \) と \( \overrightarrow{b} \) のなす角を \( \theta\quad (0^\circ \leqq \theta \leqq 180^\circ )\quad \) とすると
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}|\ |\overrightarrow{b}|\ \cos \theta \)
内積と成分
\( \overrightarrow{a}\ =\ (a_1,\ a_2),\quad \overrightarrow{b}\ =\ (b_1,\ b_2)\quad \) のとき
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b}\ =\ a_1 b_1\ +\ a_2 b_2 \)
また、\( \ \overrightarrow{a}\ \) と \( \ \overrightarrow{b}\ \) のなす角を \( \theta \) とすると
\(\displaystyle \qquad cos \theta\ =\ \dfrac{ \overrightarrow{a} \cdot \overrightarrow{b} }{ |\overrightarrow{a}|\ |\overrightarrow{b}| }\ =\ \dfrac{ a_1 b_1\ +\ a_2 b_2 }{ \sqrt{ {a_1}^2\ +\ {a_2}^2 }\ \sqrt{ {b_1}^2\ +\ {b_2}^2 } } \)
内積と平行・垂直条件
\( \overrightarrow{a}\ =\ (a_1,\ a_2)\ \neq\ \overrightarrow{0},\quad \overrightarrow{b}\ =\ (b_1,\ b_2)\ \neq\ \overrightarrow{0}\ \) とする。
- 平行条件
- \( \overrightarrow{a}\ // \overrightarrow{b}\quad \Longleftrightarrow\quad \overrightarrow{a}\ \cdot \overrightarrow{b}\ =\pm |\ \overrightarrow{a}\ |\ |\ \overrightarrow{b}\ |\quad \Longleftrightarrow\quad a_1 b_2\ -\ a_2 b_1\ =\ 0 \)
- 垂直条件
- \( \overrightarrow{a}\ \perp\ \overrightarrow{b}\quad \Longleftrightarrow\quad \overrightarrow{a}\ \cdot \overrightarrow{b}\ =\ 0\quad \Longleftrightarrow\quad a_1 b_1\ +\ a_2 b_2\ =\ 0 \)
位置ベクトルと共線条件
分点の位置ベクトル
2点 \( A (\overrightarrow{a}), B (\overrightarrow{b}) \) に対して、線分 \( AB \) を \( m : n \) に分ける点の位置ベクトル。
- 内分
- \(\displaystyle \dfrac{ n \overrightarrow{a} + m \overrightarrow{b} }{ m + n} \)
- 外分
- \(\displaystyle \dfrac{ -\ n \overrightarrow{a} + m \overrightarrow{b} }{ m\ -\ n} \)
共線条件
2点 \( A, B \) が異なるとき
点 \( P \) が直線 \( AB \) 上にある \( \quad \Longleftrightarrow \quad \overrightarrow{AP} = k \overrightarrow{AB} \) となる実数 \( k \) がある
ベクトル方程式
直線上の任意の点 \( P \) の位置ベクトルを \( \overrightarrow{p} \) とし、\( s, t \) を実数の変数とする。
直線のベクトル方程式
- 点 \( A ( \overrightarrow{a} ) \) を通り、\( \overrightarrow{d} (\neq \overrightarrow{0} ) \) に平行な直線のベクトル方程式
\( \qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d} \) - 異なる2点 \( A (\overrightarrow{a}),\ B (\overrightarrow{b}) \) を通る直線のベクトル方程式
\( \qquad \overrightarrow{p} = (1\ -\ t) \overrightarrow{a} + t \overrightarrow{b} \qquad \) または
\( \qquad \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b}, \quad s + t = 1 \)
内積による直線のベクトル方程式
点 \( A (\overrightarrow{a} ) \) を通り、\( \overrightarrow{n} (\neq \overrightarrow{0}) \) に垂直な直線のベクトル方程式
\( \qquad \overrightarrow{n} \cdot ( \overrightarrow{p}\ -\ \overrightarrow{a} ) = 0 \)
平面上の点の存在範囲
\( \triangle OAB \) に対して、\( \overrightarrow{OP} = s \overrightarrow{OA} + t \overrightarrow{OB} \) のとき、点 \( P \) の存在範囲は
- 直線 \( AB \quad \Longleftrightarrow \quad s + t = 1 \)
特に 線分 \( AB \quad \Longleftrightarrow \quad s + t = 1,\; s \geqq 0,\; t \geqq 0 \) - \( \triangle OAB \) の周と内部 \( \quad \Longleftrightarrow \quad 0 \leqq s + t \leqq 1,\; s \geqq 0,\; t \geqq 0 \)
- 平行四辺形 \( OACB \) の周と内部 \( \quad \Longleftrightarrow \quad 0 \leqq s \leqq 1,\; 0 \leqq t \leqq 1 \)
円のベクトル方程式
中心 \( C (\overrightarrow{c}) \)、半径 \( r \) の円のベクトル方程式
\( \qquad |\ \overrightarrow{p}\ -\ \overrightarrow{c}\ | = r \)
ベクトルの応用
点 \( P \) が直線 \( AB \) 上にある \( \quad \Longleftrightarrow \quad \overrightarrow{OP} = s \overrightarrow{OA} + t \overrightarrow{OB},\; s + t = 1 \) となる実数 \( s,\; t \) がある。
空間のベクトル
ベクトルの演算、相当、大きさ
ベクトルの分解
同じ平面上にない4点 \( O, A, B, C \) に対して \( \overrightarrow{OA} = \overrightarrow{a},\ \overrightarrow{OB} = \overrightarrow{b},\ \overrightarrow{OC} = \overrightarrow{c}\ \) とすると、任意のベクトル \(\ \overrightarrow{p}\ \) は実数 \(\ s, t, u\ \) を用いてただ一通りに \(\ \overrightarrow{p} = s \overrightarrow{a} + t \overrightarrow{b} + u \overrightarrow{c}\ \) の形に表される。
相当、大きさ
\( \overrightarrow{a}\ =\ (a_1,\ a_2,\ a_3),\ \overrightarrow{b}\ =\ (b_1,\ b_2,\ b_3)\ \) とする。
\( \qquad \overrightarrow{a}\ =\ \overrightarrow{b} \qquad \Longleftrightarrow \qquad a_1 = b_1,\ a_2 = b_2,\ a_3 = b_3 \)
\( \qquad |\overrightarrow{a}|\ =\ \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\)
\( \overrightarrow{AB} \) の成分と大きさ
\( A (a_1,\ a_2,\ a_3),\ B (b_1,\ b_2,\ b_3)\ \) のとき
\( \qquad \overrightarrow{AB}\ =\ ( b_1 – a_1,\ b_2 – a_2,\ b_3 – a_3 ) \)
\( \qquad |\overrightarrow{AB}|\ =\ \sqrt{(b_1 – a_1)^2 + (b_2 – a_2)^2 + (b_3 – a_3)^2 } \)
ベクトルの内積
\( \overrightarrow{a}\ =\ (a_1,\ a_2,\ a_3),\ \overrightarrow{b}\ =\ (b_1,\ b_2,\ b_3)\ \) のとき
\( \qquad \overrightarrow{a} \cdot \overrightarrow{b}\ =\ a_1 b_1\ +\ a_2 b_2\ +\ a_3 b_3 \)
ベクトルの応用
同じ平面上にある条件
\( s, t, u \) を実数とする。
点 \( P ( \overrightarrow{p} ) \) が3点 \( A ( \overrightarrow{a} ),\ B ( \overrightarrow{b} ),\ C ( \overrightarrow{c} )\ \) の定める平面上にある
\( \qquad \Longleftrightarrow \quad \overrightarrow{CP}\ =\ s \overrightarrow{CA} + t \overrightarrow{CB} \)
\( \qquad \Longleftrightarrow \quad \overrightarrow{p}\ =\ s \overrightarrow{a} + t \overrightarrow{b} + u \overrightarrow{c}, \qquad s + t + u = 1 \)
球面の方程式
- 点 \( (a, b, c) \) を中心とする 半径 \( r \) の球面
\( \qquad (x\ -\ a)^2\ +\ (y\ -\ b)^2\ +\ (z\ -\ c)^2\ =\ r^2 \)
特に、原点を中心とする 半径 \( r \) の球面
\( \qquad x^2\ +\ y^2\ +\ z^2\ =\ r^2 \) - 一般形 \(\qquad x^2\ +\ y^2\ +\ z^2\ +\ Ax\ +\ By\ +\ Cz\ +\ D\ =\ 0 \)
ただし、\(\qquad A^2\ +\ B^2\ +\ C^2\ -\ 4D\ \gt\ 0 \) - 中心が \(\ C(\overrightarrow{c})\ \)、半径が \( r \) の球面ベクトル方程式 \( \qquad | \overrightarrow{p}\ -\ \overrightarrow{c} |\ =\ r\)
(参考) 平面・直線の方程式
平面の方程式
- 点 \( A ( \overrightarrow{a} ) \) を通り、\( n (\neq 0 ) \) に垂直な平面のベクトル方程式 \( \qquad \overrightarrow{n} \cdot (\overrightarrow{p}\ -\ \overrightarrow{a})\ =\ 0 \)
- \( A (x_1,\ y_1,\ z_1),\ \overrightarrow{n}\ =\ (a,\ b,\ c) \) のとき、平面の方程式 \( \qquad a (x\ -\ x_1)\ +\ b (y\ -\ y_1)\ +\ c (z\ -\ z_1)\ =\ 0 \)
- 平面の方程式の一般形 \(\qquad ax\ +\ by\ +\ cz\ + d\ =\ 0 \)
直線の方程式
\( t \) を実数とする。
- 点 \( A (\overrightarrow{a} ) \) を通り、\( \overrightarrow{d} (\neq \overrightarrow{0}) \) に平行な直線ベクトル方程式 \( \qquad \overrightarrow{p} = \overrightarrow{a} + t \overrightarrow{d}\)
- \( A (x_1,\ y_1,\ z_1),\ \overrightarrow{d} = (l,\ m,\ n) \) のとき、直線の方程式
- \( x\ =\ x_1\ +\ lt,\ y\ =\ y_1\ +\ mt,\ z\ =\ z_1\ +\ nt \)
- \(\displaystyle \dfrac{ x\ -\ x_1 }{l}\ =\ \dfrac{ y\ -\ y_1 }{m}\ =\ \dfrac{ z\ -\ z_1 }{n} \qquad (lmn\ \neq\ 0) \)
複素数平面
複素数平面
絶対値と2点間の距離
- 定義
- \( z = a + b i\ \) に対し \(\ |z|\ =\ \sqrt{a^2 + b^2} \)
- 絶対値の性質
- \( z,\ \alpha,\ \beta \) は複素数とする。
\( \qquad |z|\ =\ 0 \quad \Longleftrightarrow \quad z\ =\ 0 \)
\( \qquad |z|\ =\ |-z|\ =\ |\bar{z}|,\ z \bar{z}\ =\ |z|^2 \)
\( \qquad |\alpha \beta|\ =\ |\alpha| |\beta|\)
\(\displaystyle \qquad \left| \dfrac{\alpha}{\beta} \right|\ =\ \dfrac{|\alpha|}{|\beta|} \qquad (\beta\ \neq\ 0) \) - 2点 \(\ \alpha,\ \beta\ \) 間の距離
- \( | \beta\ -\ \alpha | \)
複素数の極形式
複素数平面上で、\(\ O(0),\ P(z),\ z\ =\ a\ +\ bi\ \ (\neq\ 0),\ OP\ =\ r,\ OP\) と実軸の正の部分とのなす角が \(\ \theta\ \) のとき、
\( \qquad z\ =\ r (\cos{\theta}\ + i \sin{\theta}) \quad (r\ \gt\ 0) \)
複素数の乗法、除法
\( z_1\ =\ r_1 (\cos{\theta_1}\ + i \sin{\theta_1}),\ z_2\ =\ r_2 (\cos{\theta_2}\ + i \sin{\theta_2})\ \) とする。
- 複素数 \(\ z_1,\ z_2\ \) の乗法
- \( z_1 z_2\ =\ r_1 r_2 \{ cos( \theta_1\ +\ \theta_2 )\ +\ i \sin( \theta_1\ +\ \theta_2 ) \} \)
- \( \qquad |z_1 z_2|\ =\ |z_1| |z_2|, \quad arg\ z_1 z_2\ =\ arg\ z_1\ +\ arg\ z_2 \)
- 複素数 \(\ z_1,\ z_2\ \) の除法 ( \( z_2\ \neq\ 0\ \) とする)
- \( \displaystyle \dfrac{z_1}{z_2}\ =\ \dfrac{r_1}{r_2} \{ cos( \theta_1\ -\ \theta_2 )\ +\ i \sin( \theta_1\ -\ \theta_2 ) \} \)
- \( \displaystyle \qquad \left| \dfrac{z_1}{z_2} \right|\ =\ \dfrac{|z_1|}{|z_2|}, \quad arg \dfrac{z_1}{z_2}\ =\ arg\ z_1\ -\ arg\ z_2 \)
- \( m:n \) に内分する点
- \( \dfrac{ n \alpha\ +\ m \beta }{ m\ +\ n } \)
- 中点
- \( \dfrac{ \alpha\ +\ \beta }{ 2 } \)
- \( m:n \) に外分する点
- \( \dfrac{ -n \alpha\ -\ m \beta }{ m\ +\ n } \)
- \( |z\ -\ \alpha|\ =\ r \quad (r\ \gt\ 0) \)
- 中心 \( A \)、半径 \( r \) の円
- \( n |z\ -\ \alpha|\ =\ m |z\ -\ \beta|, \quad n\ \gt\ 0,\ m\ \gt\ 0 \)
-
- \( m\ =\ n \) のとき
- 線分 \( AB \) の垂直二等分線
- \( m\ \neq\ n \) のとき
- 線分 \( AB \) を \( m:n \) に内分する点と外部する点を直径の両端とする円 (アポロニウスの円)
- \( \angle \beta \alpha \gamma\ =\ \arg{ \dfrac{\gamma\ -\ \alpha}{\alpha\ -\ \alpha} } \)
- 3 点\( A,\ B,\ C\ \) が一直線上にある \( \quad \Longleftrightarrow \quad \dfrac{ \gamma\ -\ \alpha }{ \beta\ -\ \alpha } \) が実数
- \( AB\ \perp\ AC \quad \Longleftrightarrow \quad \dfrac{ \gamma\ -\ \alpha }{ \beta\ -\ \alpha } \) が純虚数
- \( AB \perp CD \quad \Longleftrightarrow \quad \dfrac{ \delta\ -\ \gamma }{ \beta\ -\ \alpha } \) が純虚数
- \( AB /\!/ CD \quad \Longleftrightarrow \quad \dfrac{ \delta\ -\ \gamma }{ \beta\ -\ \alpha } \) が実数
- 放物線
- \(\displaystyle y^2 = 4px \qquad \to \qquad y_1y = 2p(x + x_1) \)
- 楕円
- \(\displaystyle \dfrac{x^2}{a^2}\ +\ \dfrac{y^2}{b^2}\ =\ 1 \qquad \to \qquad \dfrac{x_1 x}{a^2}\ +\ \dfrac{y_1 y}{b^2}\ =\ 1 \)
- 双曲線
- \(\displaystyle \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ 1 \qquad \to \qquad \dfrac{x_1 x}{a^2}\ -\ \dfrac{y_1 y}{b^2}\ =\ 1 \)
- \( 0 \lt e \lt 1 \) のとき
- \( F \) を焦点の1つとする楕円
- \( e = 1 \) のとき
- \( F \) を焦点、\( l \) を準線とする放物線
- \( e \gt 1 \) のとき
- \( F \) を焦点の1つとする双曲線
- 円
- \(\displaystyle x\ =\ a \cos{\theta},\quad y\ =\ a \sin{\theta} \qquad\qquad \to \qquad x^2\ +\ y^2\ =\ a^2 \)
- 放物線
- \(\displaystyle x\ =\ pt^2,\quad y\ =\ 2pt \qquad\qquad \to \qquad y^2\ =\ 4px \)
- 楕円
- \(\displaystyle x\ =\ a \cos{\theta},\quad y\ =\ b \sin{\theta} \qquad\qquad \to \qquad \dfrac{x^2}{a^2}\ +\ \dfrac{y^2}{b^2}\ =\ 1 \)
- 双曲線
- \(\displaystyle x\ =\ \dfrac{ a }{ \cos{\theta} },\quad y\ =\ b \tan{\theta} \qquad\qquad \to \qquad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2}\ =\ 1 \)
- サイクロイド
- \(\displaystyle x\ =\ a (\theta\ -\ \sin{\theta}),\quad y\ =\ a (1 -\ \cos{\theta}) \)
- \( x\ =\ r \cos {\theta},\quad y\ =\ r \sin {\theta} \)
- \( r\ =\ \sqrt{x^2\ +\ y^2} \)
\( r \neq 0 \) のとき \(\displaystyle \quad \cos {\theta}\ =\ \dfrac{x}{r},\quad \sin {\theta}\ =\ \dfrac{y}{r} \) - 円
- 中心が極、半径 \( a \) : \(\displaystyle \qquad r = a\)
中心 \(\ (a,\ 0)\ \)、半径 \( a \) : \(\displaystyle \qquad r = 2a \cos{\theta}\)
中心 \(\ (r_0,\ {\theta}_0)\ \)、半径 \( a \) : \(\displaystyle \qquad r^2\ -\ 2r r_0 \cos{( \theta\ -\ {\theta}_0 )}\ +\ {r_0}^2\ =\ a^2 \) - 直線
- 極を通り、始線と \( \alpha \) の角をなす: \(\displaystyle \qquad \theta\ =\ \alpha \)
点 \(\ A(a,\ \alpha)\ \) を通り、\( OA \) ( \( O \) は極) に垂直: \(\displaystyle \qquad r \cos{(\theta\ -\ \alpha)}\ =\ a\qquad (a\ \gt\ 0) \) - 2次曲線
- 焦点を極とすると \(\displaystyle \qquad r(1\ +\ e \cos{\theta})\ =\ l\quad (a\ \gt\ 0) \)
\(\displaystyle \qquad 0\ \lt\ e\ \lt\ 1\ \) のとき 楕円
\(\displaystyle \qquad e\ =\ 1\ \) のとき 放物線
\(\displaystyle \qquad 1\ \lt\ e\ \) のとき 双曲線
となる。
複素数の乗法と回転
\( P(z),\ r\ \gt\ 0\ \) とする。
点 \(\ r ( \cos{\theta}\ +\ \sin{\theta} ) \cdot z\ \) は、点 \( P \) を原点を中心として角 \( \theta \) だけ回転し、原点からの距離を \( r \) 倍した点である。
ド・モアブルの定理
ド・モアブルの定理
\( n \) が整数のとき
\( \qquad (\cos{\theta}\ +\ i \sin{\theta})^n\ =\ \cos{n \theta} + i \sin{n \theta}\)
\( 1 \) の \( n \) 乗根
\( 1 \) の \( n \) 乗根は \( n \) 個あり、それらを
\( \qquad z_k\ (k\ =\ 0,\ 1,\ 2,\ \cdots,\ n\ -\ 1) \)
とすると
\(\displaystyle \qquad z_k\ =\ \cos{ \dfrac{2 k \pi}{n} }\ +\ i \sin{ \dfrac{2 k \pi}{n} } \)
\( n\ \geqq\ 3\) のとき、点 \( z_k\ (k\ =\ 0,\ 1,\ 2,\ \cdots,\ n\ -\ 1) \) は点 \( 1 \) を1つの頂点として単位円に内接する正 \( n \) 角形の頂点である。
複素数と図形
点 \( A (\alpha),\ B (\beta),\ C (\gamma),\ D (\delta)\ \) は互いに異なる点とする。
線分 \( AB \) の内分点、外分点
方程式の表す図形
なす角、平行・垂直などの条件
式と曲線
2次曲線
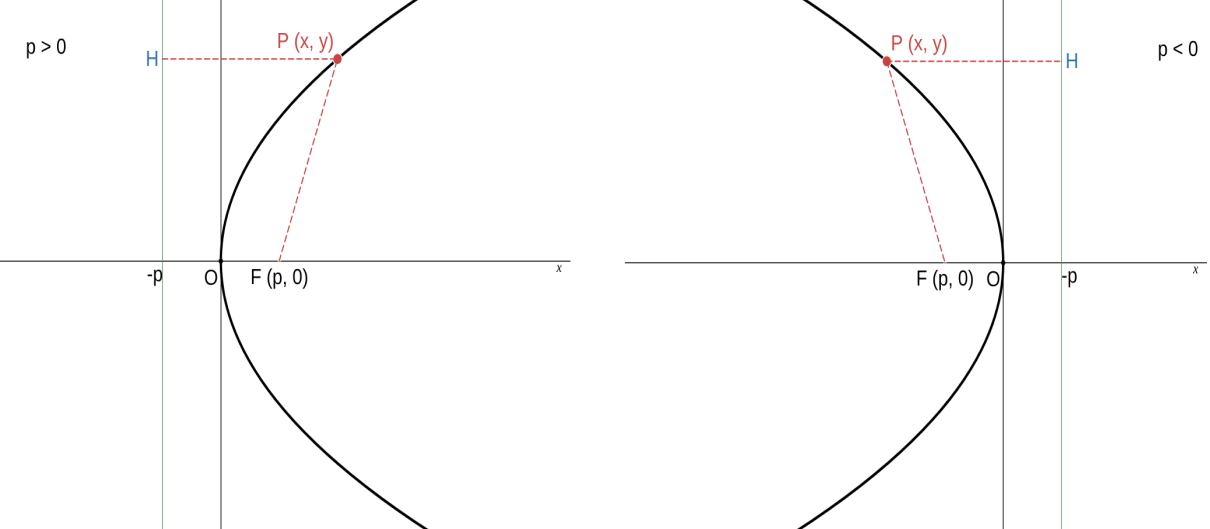
放物線 \(\qquad y^2 = 4px \quad (p \neq 0) \qquad \) [標準形]
頂点は原点、焦点は \( F\ (p,\ 0) \)、準線は直線 \( x = -p \)
軸は \( x \) 軸。曲線は軸に関して対称。
曲線上の任意の点と焦点・準線との距離は等しい。
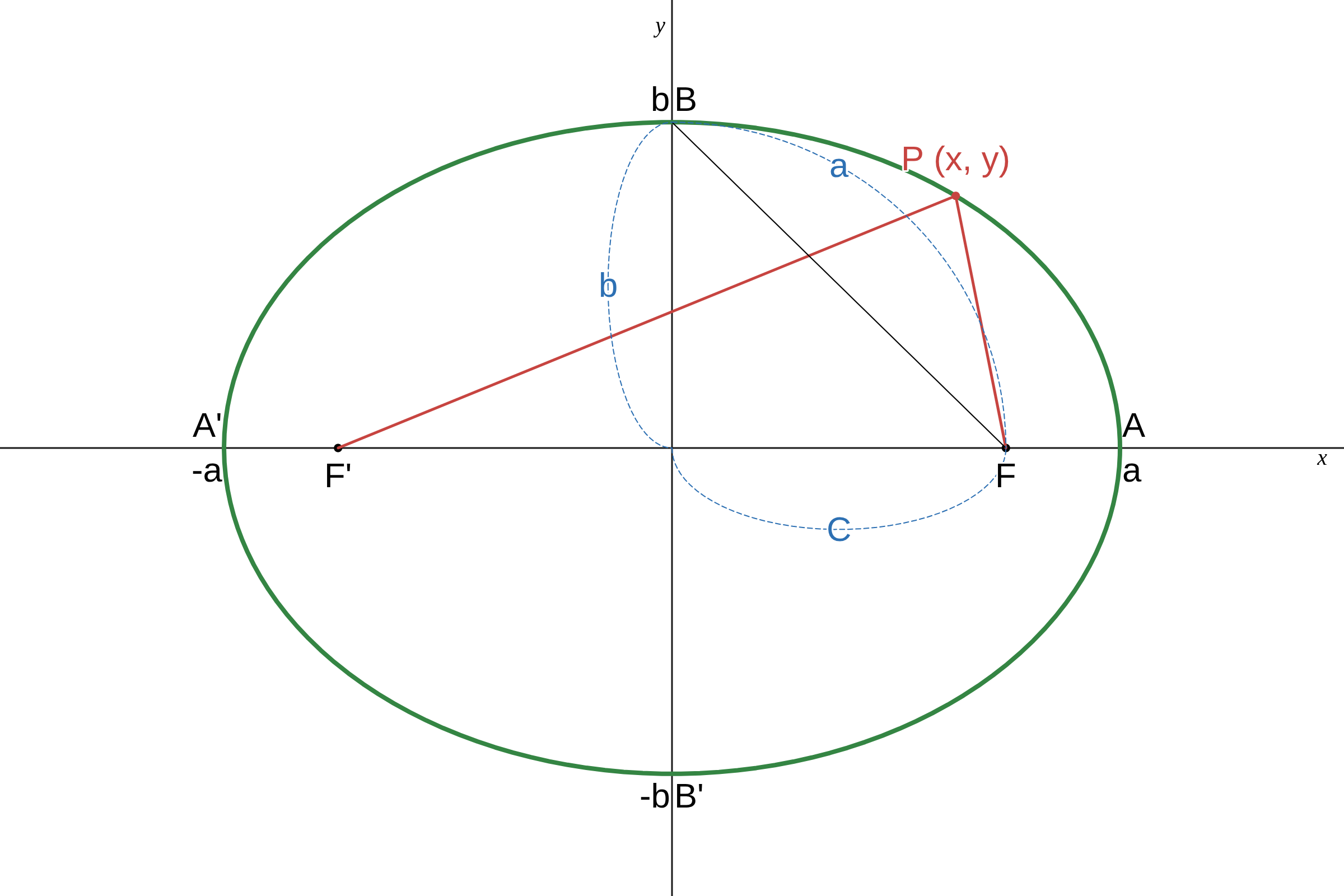
楕円 \(\displaystyle \qquad \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1 \quad (a \gt b \gt 0) \qquad \) [標準形]
中心は原点、長軸の長さは \( 2a \)、短軸の長さは \( 2b \)
焦点は \( F\ (c,\ 0) \)、\( F^\prime\ (-c,\ 0)\quad c = \sqrt{ a^2\ -\ b^2} \)
曲線は \( x \)軸、\( y \)軸、原点に関して対称。
曲線上の任意の点 \( P \) について \( PF + PF^\prime = 2a \)
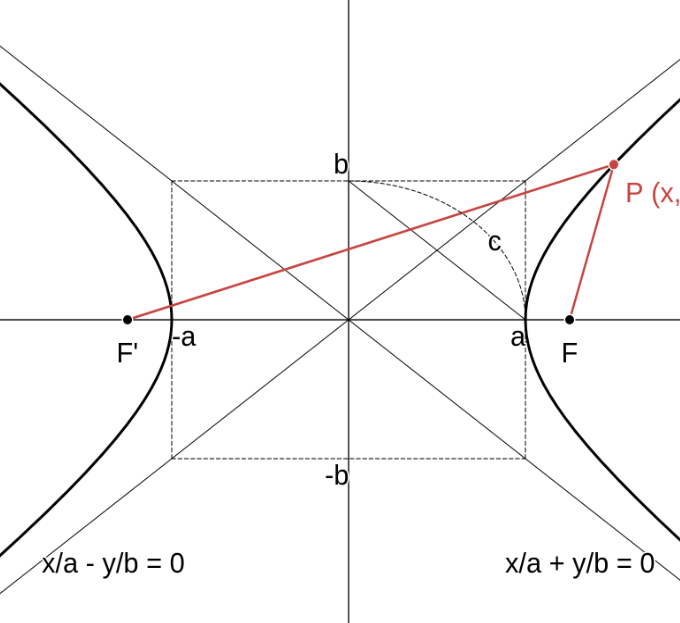
双曲線 \(\displaystyle \qquad \dfrac{x^2}{a^2}\ -\ \dfrac{y^2}{b^2} = 1 \quad ( a \gt 0,\ b \gt 0) \qquad \) [標準形]
中心は原点。曲線は \( x \) 軸、\( y \) 軸、原点に関して対称。
焦点は \( F\ (c,\ 0),\ F^\prime\ (-c,\ 0) \quad c = \sqrt{a^2 + b^2} \)
漸近線は 直線 \(\displaystyle \dfrac{x}{a}\ -\ \dfrac{y}{b} = 0,\ \dfrac{x}{a}\ +\ \dfrac{y}{b} = 0 \)
曲線上の任意の点 \( P \) について \( \quad |PF\ -\ PF^\prime| = 2a \)
 |
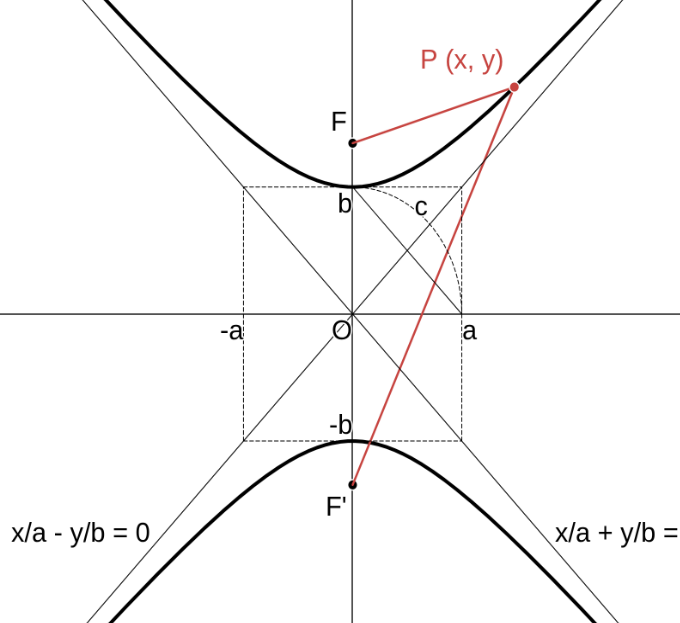 |
2次曲線の接線
曲線上の点 \( (x_1,\ y_1) \) における接線の方程式は
離心率 \( e \) と準線 \( l \)
定点 \( F \) と \( F \) を通らない定直線 \( l \) からの距離の比が \(e : 1\) である点の軌跡は
媒介変数表示
曲線の媒介変数表示
\( a\ \gt\ 0,\ b\ \gt\ 0\ \) とする。
極座標と極方程式
極座標 \(\ (r,\ \theta)\ \) と直交座標 \(\ (x,\ y)\ \) の関係
極方程式
\( r\ \lt\ 0 \) も考える。すなわち、\( r\ \gt\ 0 \) のときの点 \(\ (-r,\ \theta)\ \) は 点 \(\ (r,\ \theta + \pi)\ \) と同じ点を表す。